Last Updated on February 8, 2026 by Rajeev Bagra

---

Understanding correlation is essential in data analysis, finance, marketing, and business intelligence.

In this tutorial, you will learn:

✅ What Pearson correlation really measures
✅ Why “no correlation” happens
✅ How the formula works
✅ When Pearson fails
✅ How professionals use it in finance
✅ How to interpret graphs correctly

---

🔹 1. What Is Pearson Correlation?

The Pearson Correlation Coefficient (r) measures:

How strongly two variables move together in a straight-line pattern.

Its value lies between:

Value	Meaning
+1	Perfect positive
0	No linear relation
–1	Perfect negative

Example:

• Ads ↑ → Sales ↑ → Positive
• Rates ↑ → Loans ↓ → Negative

---

🔹 2. Important Rule: Pearson Is About X vs Y (Not Time)

Many beginners think:

“If X and Y are both straight over time, they are correlated.”

❌ This is wrong.

Pearson does NOT care about time.

It only looks at:

How Y changes when X changes.

So always think:

📌 Plot Y against X — not against time.

---

🔹 3. The Pearson Formula

What It Means in Simple Words

Correlation = (How X and Y move together) ÷ (How much they move separately)

---

🔹 4. How the Formula Detects Relationship

The key part is:

This multiplies deviations.

X moves	Y moves	Result
Up	Up	+
Down	Down	+
Up	Down	–
Down	Up	–

If many + → Positive r

If many – → Negative r

If + and – cancel → r ≈ 0

That is how “no correlation” appears.

---

📈 5. Understanding Correlation Using Graphs

Always draw a scatter plot before trusting r.

---

✅ A. Perfect Positive Correlation ( r = +1 )

Example Dataset

X	Y
1	2
2	4
3	6
4	8
5	10

Here:

All points lie on one rising line.

---

❌ B. Perfect Negative Correlation ( r = –1 )

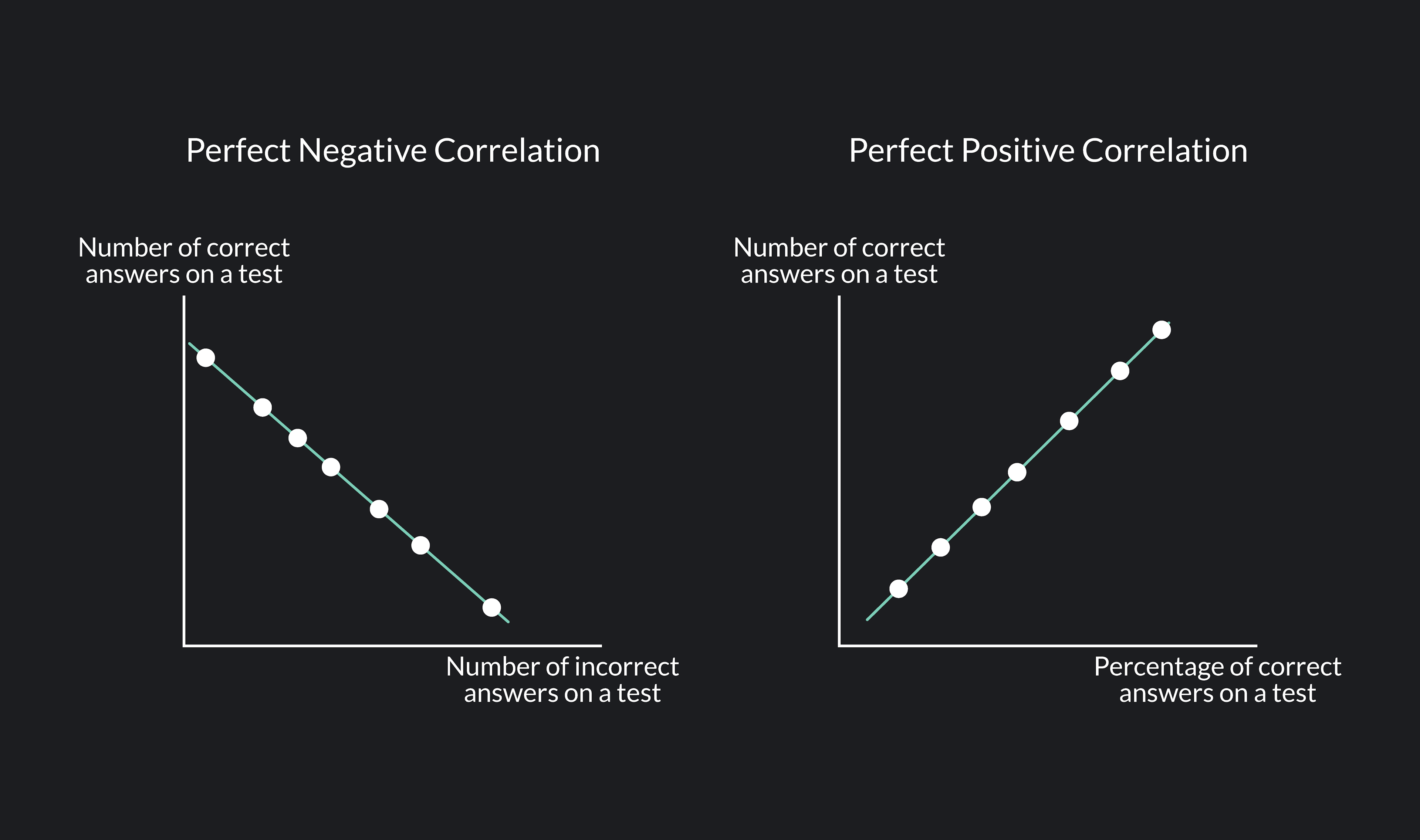
Example Dataset

X	Y
1	10
2	8
3	6
4	4
5	2

Here:

One rises, the other falls.

---

⚪ C. No Linear Correlation ( r ≈ 0 )

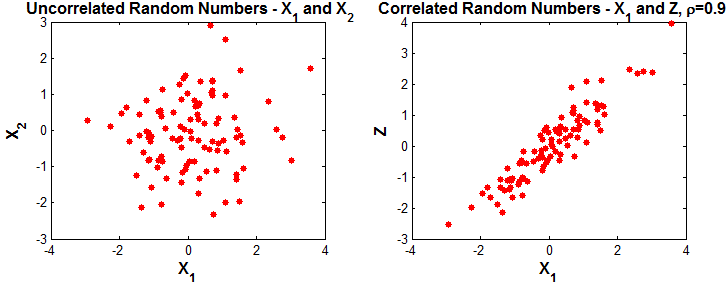
Example Dataset

X	Y
1	7
2	3
3	9
4	4
5	6

Here:

Products cancel → no straight-line pattern.

---

🔀 D. Non-Linear Relationship ( Pearson Fails )

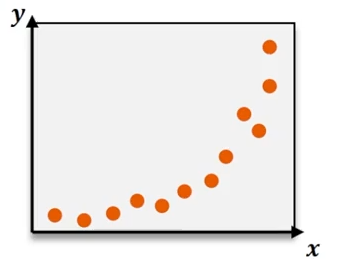
Example

X	Y
1	1
2	4
3	9
4	16
5	25

Here:

Strong relationship ❗
But Pearson → r ≈ 0 ❌

Because it is curved.

---

🔹 6. Correlation ≠ Causation

Correlation does NOT mean cause.

Example:

• Ice cream sales ↑
• Drowning ↑

Both caused by summer.

Not by each other.

---

💼 7. How Finance Professionals Use Correlation

---

🏦 A. Portfolio Diversification

Goal: Reduce risk.

r Value	Meaning
> 0.8	Risky
< 0.3	Good
< 0	Hedge

They prefer:

Campaign works.

---

🔹 8. How Professionals Decide “No Relationship”

They NEVER trust r alone.

They check:

✅ |r| < 0.2
✅ p-value > 0.05
✅ Scatter plot
✅ Stability over time
✅ Business logic

Only then:

“Probably independent.”

---

🔹 9. When NOT to Use Pearson

Do NOT use Pearson when:

❌ Data is curved
❌ Data is ranked
❌ Data has outliers
❌ Regimes change

Use instead:

• Spearman
• Regression
• Nonlinear models

---

🔹 10. Step-by-Step Method for Learners

Before using Pearson, always follow this:

Step 1

Plot X vs Y

Step 2

Ask: “Is it roughly straight?”

Step 3

If yes → Use Pearson

Step 4

Compute r

Step 5

Check if |r| > 0.3

Step 6

Interpret with business logic

---

📌 Final Summary

Topic	Key Idea
Pearson Measures	Linear relationship
r ≈ 0 Means	No straight-line pattern
Not Meaning	No relationship at all
Always Do	Plot first
Finance Use	Risk control

---

✅ Final Takeaway

Pearson correlation tells you how well two variables move together in a straight line. A value near zero means no strong linear pattern, not necessarily no relationship.